相关链接:

Abstract#

优化问题广泛存在于从制造、配送到医疗保健等各个领域。然而，大多数此类问题仍通过人工启发式方法解决，而非采用最先进的求解器进行优化求解，这是因为表述和解决这些问题所需的专业知识限制了优化工具和技术的广泛采用。本文介绍了 OptiMUS，一种基于大语言模型（LLM）的智能体，旨在根据自然语言描述来表述和解决（混合整数）线性规划问题。OptiMUS 能够建立数学模型，编写和调试求解器代码，评估生成的解决方案，并根据这些评估改进其模型和代码。OptiMUS 采用模块化结构处理问题，使其能够处理描述冗长且数据复杂的问题，而无需使用过长的提示。实验表明，在简单数据集上，OptiMUS 的性能优于现有最先进方法超过 20%；在困难数据集（包括本文发布的新数据集 NLP4LP，该数据集包含冗长且复杂的问题）上，性能提升超过 30%。

1. Introduction#

Ambiguous Terms
Long Problem Descriptions
Large Problem Data
Unreliable Outputs

Contributions#

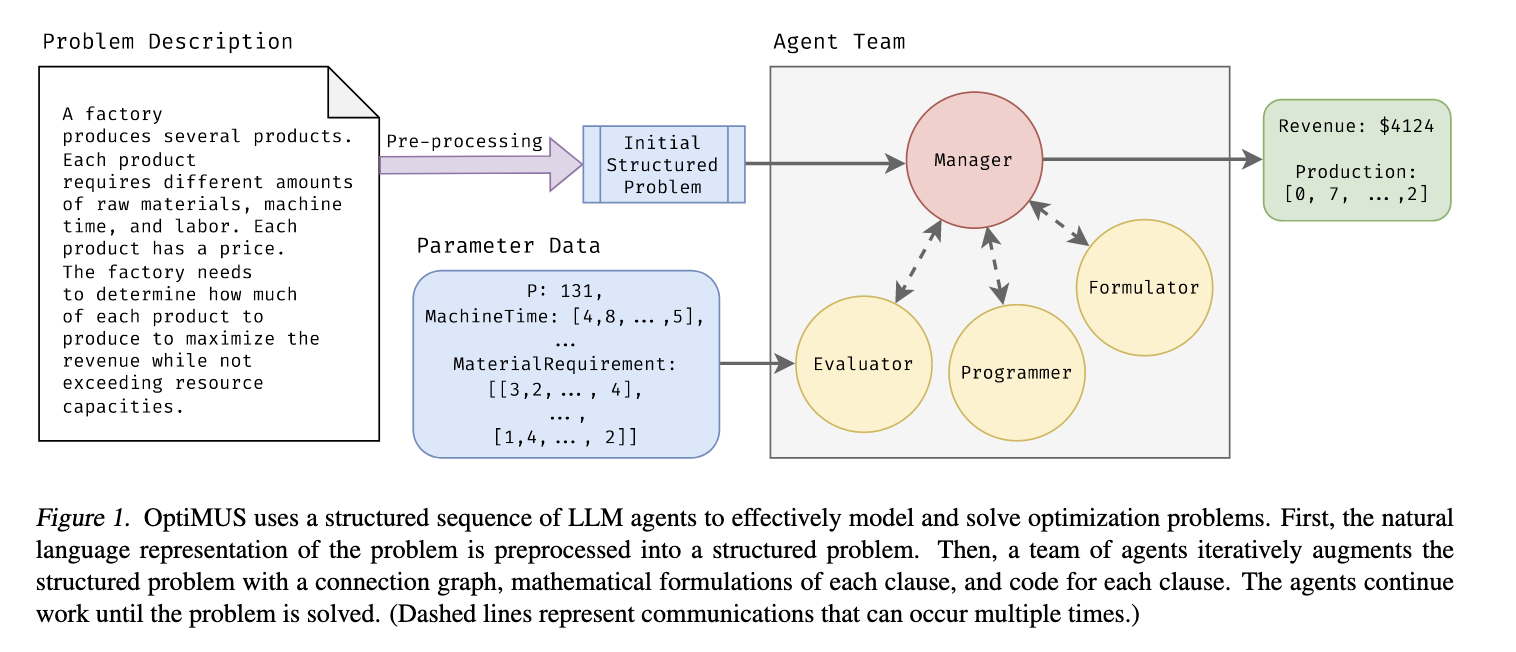
OptiMUS 使用结构化的 LLM 智能体序列来有效地建模和解决优化问题。首先，将问题的自然语言表示预处理为结构化问题。然后，一个智能体团队通过连接图、每个子句的数学公式以及每个子句的代码来迭代地增强结构化问题。智能体持续工作直到问题解决。（虚线表示可能发生多次的通信。）

现有的自然语言优化建模数据集过于简单，无法捕捉冗长问题描述和大规模问题数据的挑战。这项工作引入了 NLP4LP，一个包含 67 个复杂优化问题的开源数据集。表 1 比较了 NLP4LP 与现有数据集
开发了一个基于 LLM 的模块化智能体来建模和解决优化问题，我们称之为 OptiMUS。OptiMUS 在现有数据集上比之前最先进的方法性能高出 20% 以上，在我们更具挑战性的数据集上高出 30%。OptiMUS 采用了一种新颖的连接图，使其能够独立处理每个约束和目标。利用这个连接图，并将数据与问题描述分离，OptiMUS 能够解决描述冗长且数据文件庞大的问题，而无需过长的提示。

优化问题在数学上由目标函数和一组约束定义，一个 MILP 可以数学地写为：

minimize $\sum_{j=1}^nc_jx_j$

subject to $\begin{gathered}\sum_{j=1}^na_{ij}x_j(\leq,\quad=,\geq)b_i,i=1,\ldots m \\l_j\leq x_j\leq u_j,j=1,\ldots,n \\x_j\in\mathbb{Z},j\in\mathcal{I}\end{gathered}$

优化工作流程包括：

通过识别目标和约束，以数学形式表述优化问题
通常使用调用优化求解器的代码，根据实际数据求解问题的实现

3. Methodology#

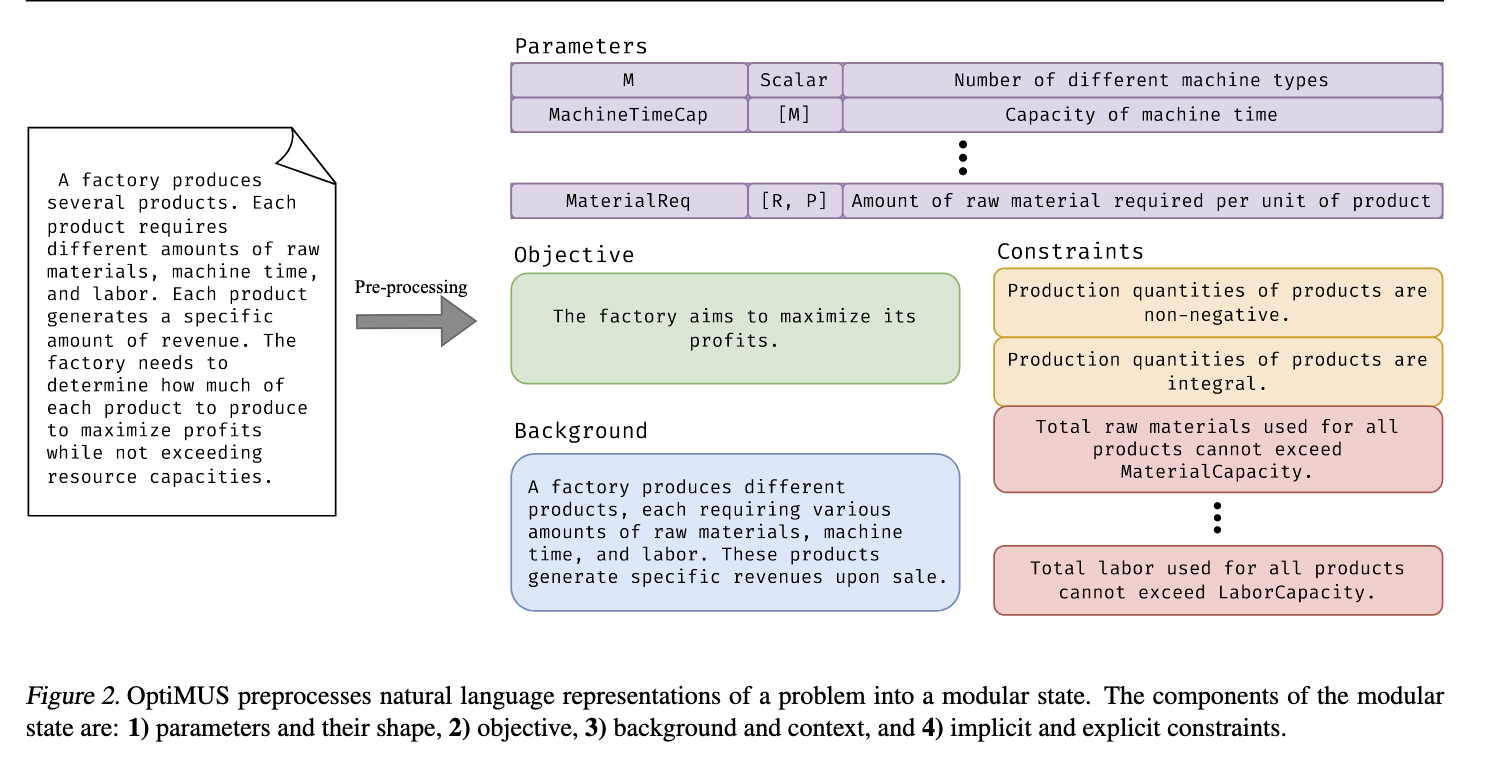
3.1 Structured Problem#

The OptiMUS preprocessor converts a natural language description of the problem into a structured problem (Figure 2) with the following components:

Parameters: 优化问题参数的列表，每个参数有三个部分
1. symbol
2. shape
3. text definition OptiMUS可以选择符号，推断形状，如果问题陈述中没有显式包含参数，则可以定义参数。
Clauses: 优化问题的子句（目标和约束）的列表。预处理器用其自然语言描述初始化每个子句。稍后，这些子句将用 LaTeX 公式和代码进行增强。
Background: 解释问题现实世界背景的短字符串。此字符串包含在每个提示中以提高常识推理能力。

The preprocessing uses three prompts:

提取参数
将问题分割为目标和约束
消除冗余、不必要以及不正确的约束

可能在第二步中存在隐性约束

3.2 Agents#

预处理后，OptiMUS 定义问题变量，表述并编码每个子句。为确保公式的一致性，OptiMUS 构建并维护一个连接图来记录每个约束中出现的变量和参数。这个连接图是 OptiMUS 性能和可扩展性的关键，因为它使 LLM 能够仅关注每个提示的相关上下文，从而生成更稳定的结果。变量列表以及 LaTeX 公式和代码最初为空；当所有子句都被表述、编程和验证后，过程即告完成。

Manager#

OptiMUS 使用一个管理器智能体来协调公式化、编程和评估的工作，认识到这些步骤可能需要重复以确保一致性和正确性。

在每个步骤中，Manager查看迄今为止的对话，并选择下一个智能体(formulator, programmer, or evaluator)来处理问题。

Manager还会生成一个任务并分配给所选智能体，例如：“检查并修复目标的公式。”

Formulator#

编写和修正变量和子句的数学公式
定义新变量和辅助约束
更新连接图中的链接

如果分配的任务是表述新的子句，公式器会遍历尚未表述的子句，并为它们生成新的公式。在此过程中，它还会在必要时定义辅助约束和新变量。此外，它决定哪些参数和变量与子句相关（见图 3）此信息用于更新连接图

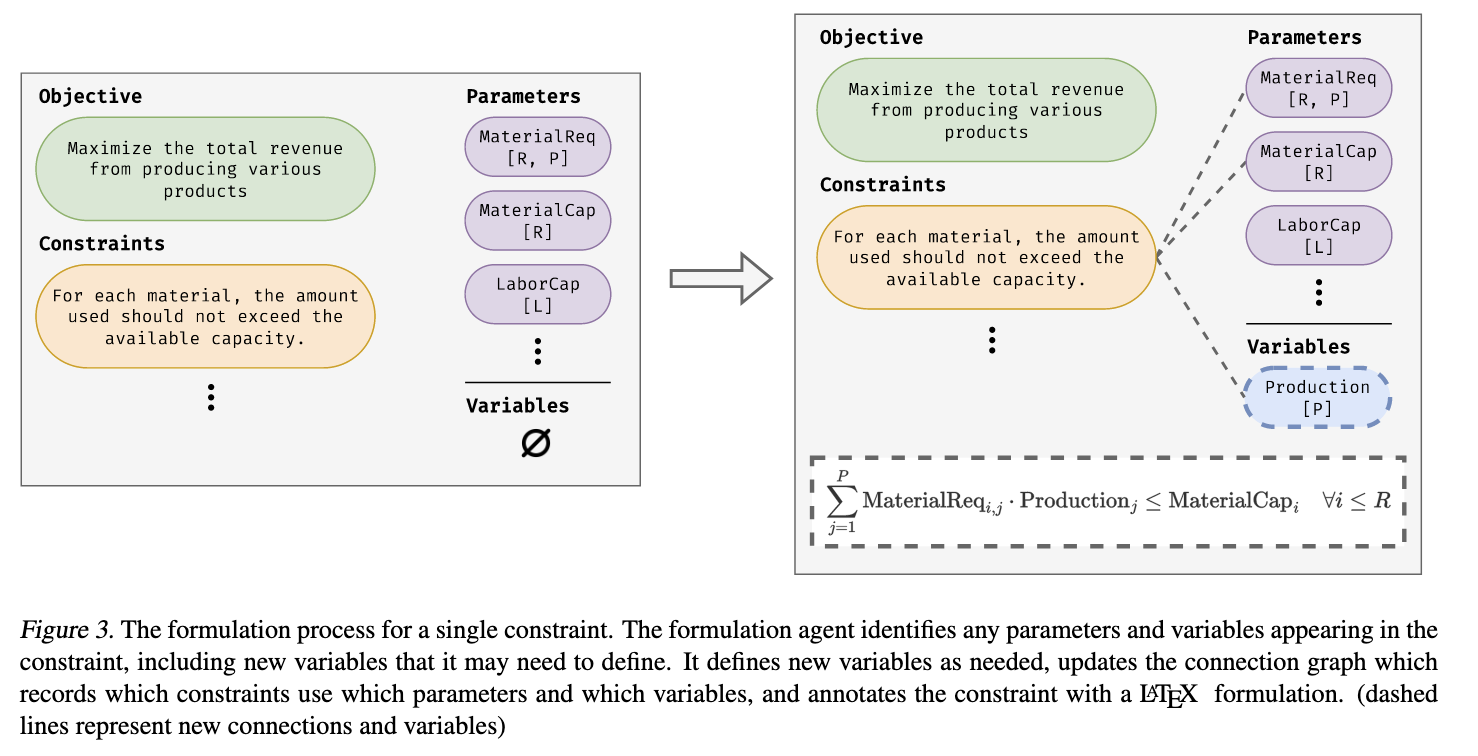
另一方面，如果任务是evaluator或programmer报告的不正确公式，该智能体会遍历标记为不正确的子句，修复它们的公式，并更新连接图。OptiMUS 还有一个额外的建模层来捕捉特殊的模型结构。

Programmer#

programmer agent的职责是编写和调试求解器代码。当programmer被manager调用时，它首先读取任务。

如果任务是为新子句编程，该智能体会遍历尚未编码的子句，并根据它们的公式生成代码。
如果任务是修复评估员报告的不正确公式，该智能体会遍历标记为有问题的子句，并修复它们的代码。

programmer使用 Python 作为编程语言，Gurobi 作为求解器。只要 LLM 支持，OptiMUS 可以针对其他求解器和编程语言。

Evaluator#

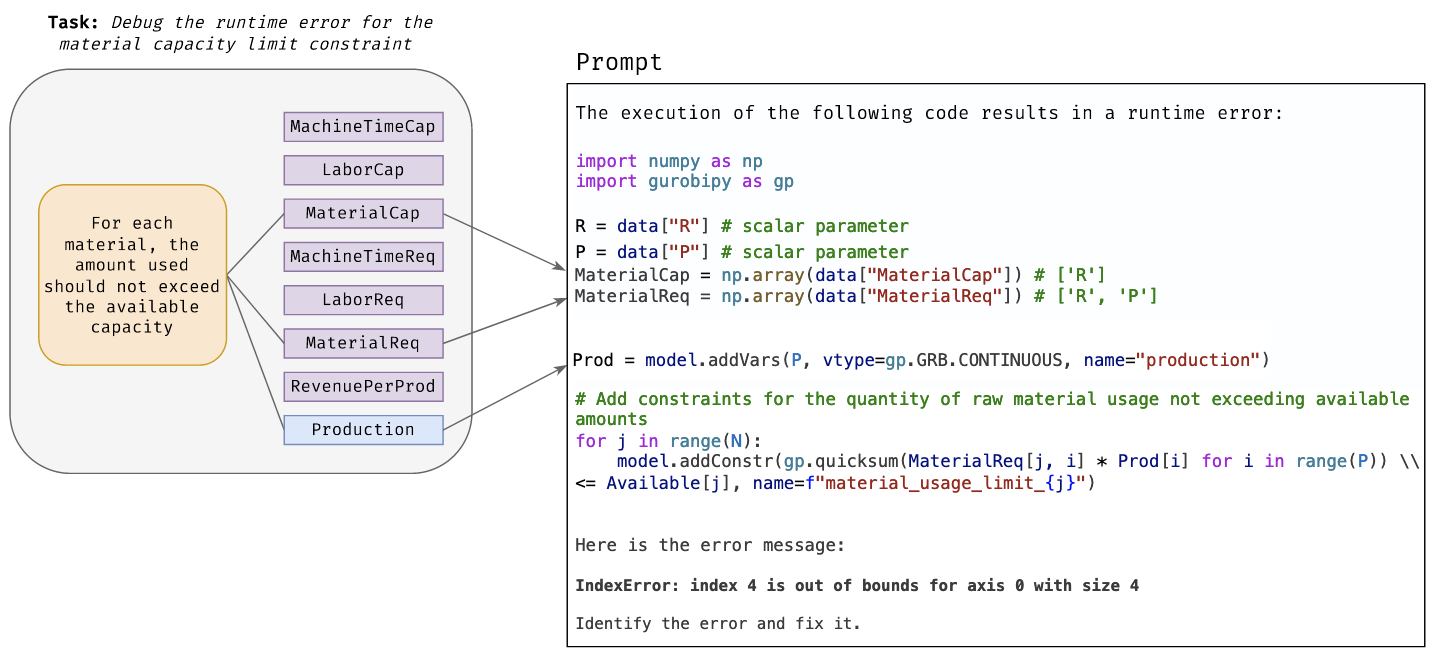
evaluator agent的职责是在数据上执行生成的代码，并识别执行期间发生的任何错误。如果evaluator遇到运行时错误，它会用有问题的代码标记变量或子句，并向manager回应适当的错误解释。该信息稍后将被其他agent用于修复公式和调试代码。

3.3 The connection graph#

OptiMUS 在约束、目标、参数和变量上维护一个连接图。OptiMUS 使用此图来检索每个提示的相关上下文，从而保持提示简短。此图也用于生成和调试代码以及纠正错误的公式。

4. Experiments#

4.1 Datasets#

NL4OPT
ComplexOR
NLP4LP

4.2 Overall Performance#

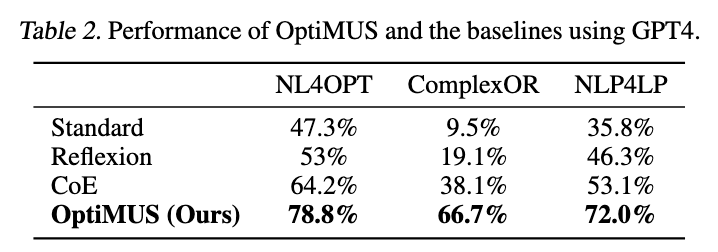
文献中使用了三个主要指标：准确率、编译错误（CE）率和运行时错误（RE）率。然而，一种方法可能生成一个完全无关但能运行的短代码，或者通过完全删除代码的相关部分来修复运行时和编译错误。因此，我们只比较模型的准确率。

结果如表 2 所示，OptiMUS 在所有数据集上都以显著优势优于所有其他方法。

4.3 Ablation Study#

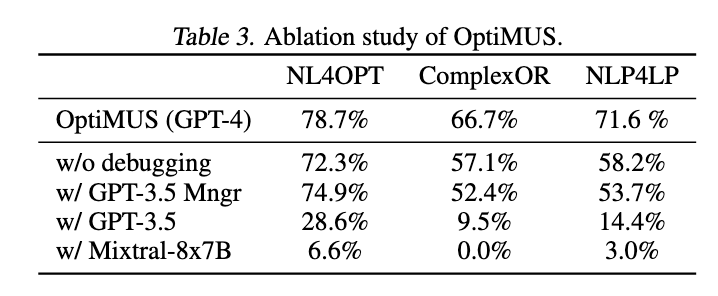
表 3 显示了调试和 LLM 选择对 OptiMUS 性能的影响。一个有趣的观察是，当使用较小的 LLMs 代替 GPT-4 时，会出现显著的性能下降。

第一个原因是 OptiMUS 的提示平均比其他方法更长，并且涉及更复杂的推理。较小的 LLMs 在推理方面较差
第二个原因是 OptiMUS 提示词的新颖和模块化结构。其他方法中使用的提示词大多遵循公共领域中丰富的问题回答格式；然而，在 OptiMUS 中，提示词更复杂，且在人际交互中不常见。较小的 LLMs 泛化和推理能力有限，因此在此类提示词上表现不佳。

还评估了 OptiMUS 的一个版本，该版本对manager使用 GPT-3.5，对其他agent使用 GPT-4。在 NL4OPT 中，性能差异很小。原因是 NL4OPT 的大多数实例都是通过简单的公式化-编程-评估链解决的。然而，在需要智能体之间更复杂交互的 ComplexOR 和 NLP4LP 中，管理器的重要性变得更加明显。

此外，还进行了禁用programmer agent’s debugging功能的实验。与manager类似，我们发现调试在更复杂的数据集中更为重要。

4.4 Sensitivity Analysis#

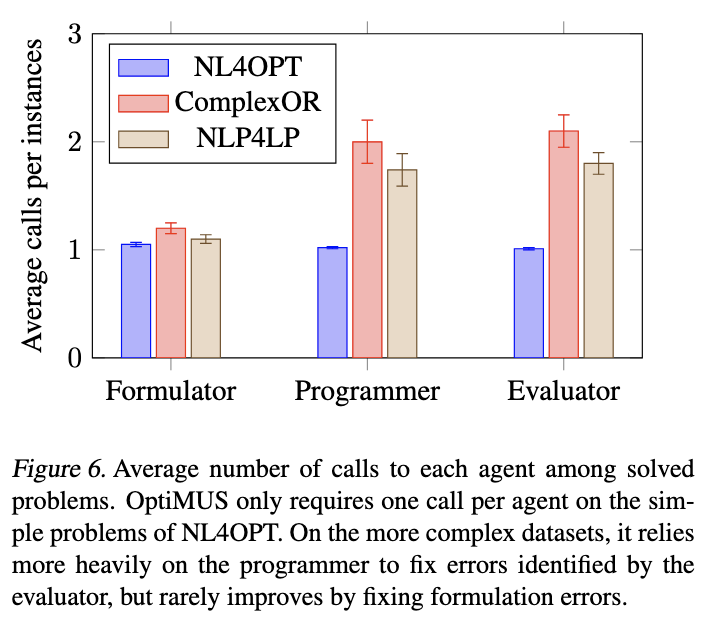
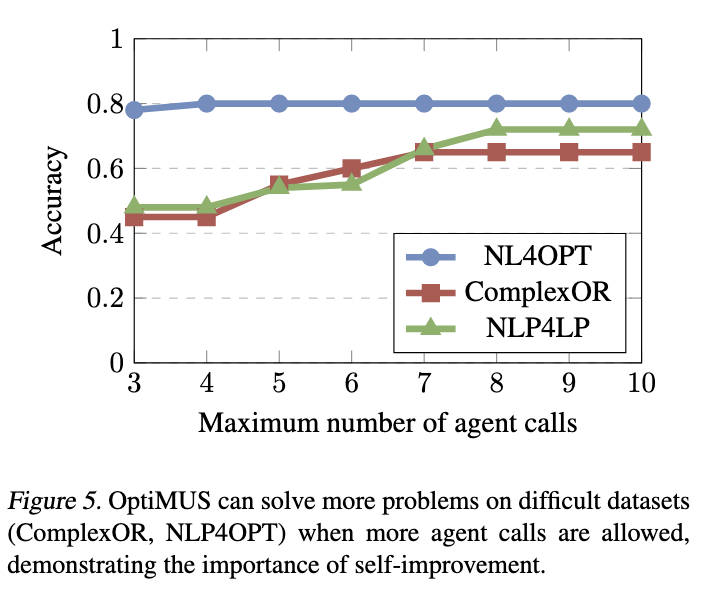
图 5 显示了manager被允许选择agent的最大次数如何影响准确率。对于 NL4OPT，大多数问题通过仅选择formulator、programmer和evaluation agent各一次来解决。然而，对于 ComplexOR 和 NLP4LP，OptiMUS 经常在开始时犯错，并通过多次选择其他agent来迭代修复它们。

此外，programmer和evaluation agent被选中的频率高于formulator。这种偏差是合理的:

编码错误更常见。LLMs 经常生成带有易于修复的微小错误的代码。
编码错误更容易识别和修复。相比之下，识别公式中的错误需要更深入的推理，并且更难。因此，OptiMUS 中的管理器被提示优先考虑修复代码，然后再考虑公式中的错误。

表 4 显示了 OptiMUS 和 CoE 针对不同数据集的平均提示长度。观察到 OptiMUS 的提示长度在不同数据集间几乎没有变化，而 CoE 的提示长度在更具挑战性的数据集上增加。原因是模块化方法允许 OptiMUS 为每个 LLM 调用提取和处理仅相关的上下文。与非模块化方法不同，OptiMUS 可以扩展到更大和更长的问题。

4.5 Failure Cases#

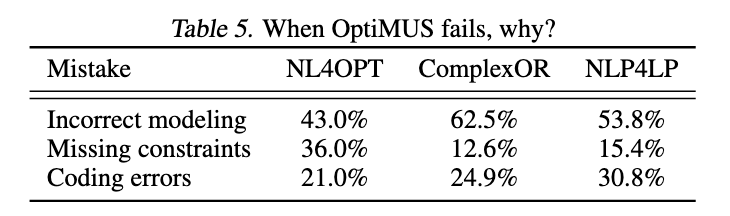
缺失或错误的约束
错误的模型：OptiMUS 使用错误的数学模型来处理问题
编码错误：即使经过调试，OptiMUS 也无法生成无错误的代码。

将失败率归一化，总和为 1.0。在问题更复杂的数据集上，错误建模更常见，而在较简单的数据集 NLP4OPT 上，模型出错的可能性较小。

理解和解释问题对于 LLMs 来说也是具有挑战性的，导致公式中存在缺失约束和错误约束。微调可能会提高 LLMs 在此任务上的性能，是未来研究的一个重要方向。

5. Conclusion#

为了展示 OptiMUS 的性能，作者发布了 NLP4LP，一个包含冗长且具有挑战性的优化问题的数据集，以展示 OptiMUS 中实施的技术的有效性。

附录#

A. Optimization Techniques#

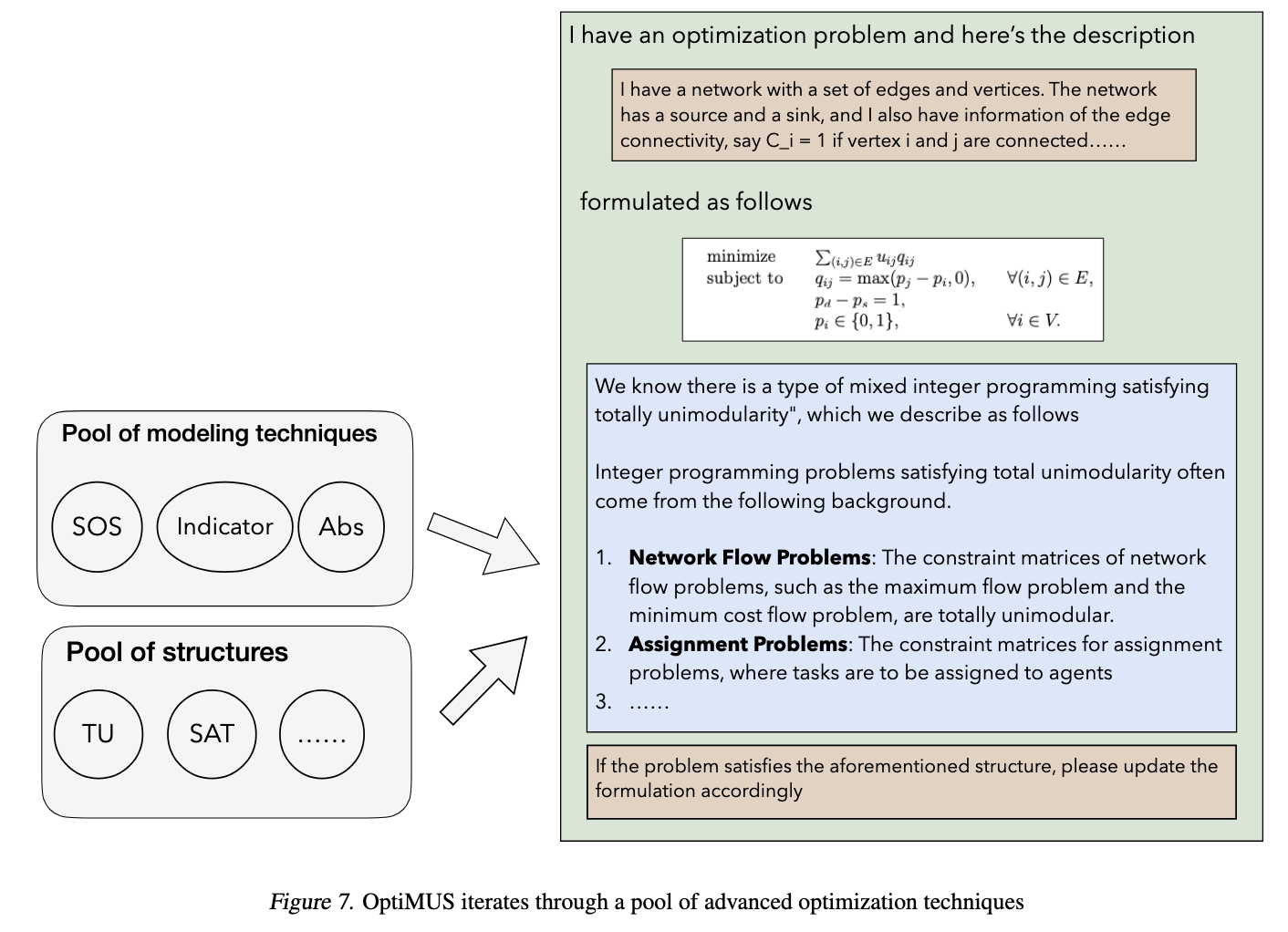
优化求解器在求解MILPs问题时利用特定于问题的结构来提高性能，并且通常为这些特殊结构提供定制的接口。使用接口不仅降低了辅助变量或约束的复杂性（以及潜在的错误），而且还告知求解器存在可以用来更快地解决问题的结构。

此外，当这些结构在模型中没有signaled时，求解器的性能会受到影响。例如，在重新表述指示变量时，big-M 系数的选择不当会降低线性松弛的强度。

虽然最先进的优化求解器可以自动检测某些问题结构，但在问题表述过程中指定结构效果更好。因此，促使formulator利用先进的优化技术和结构，包括：

Special Ordered Set
Indicator variable
General constraints
SAT and constraint programming problem
Totally unimodular problem detection

OptiMUS 迭代一系列”cheatsheet” prompts（图7），每个prompt对应于这些结构中的一个。在每个prompt中，LLM都提供了结构的描述，并通过一个示例解释了如何利用该结构。agent被要求决定该结构是否可以应用于现有formulation。在确定适当的结构后，调整formulation以在可用时利用定制的求解器接口。